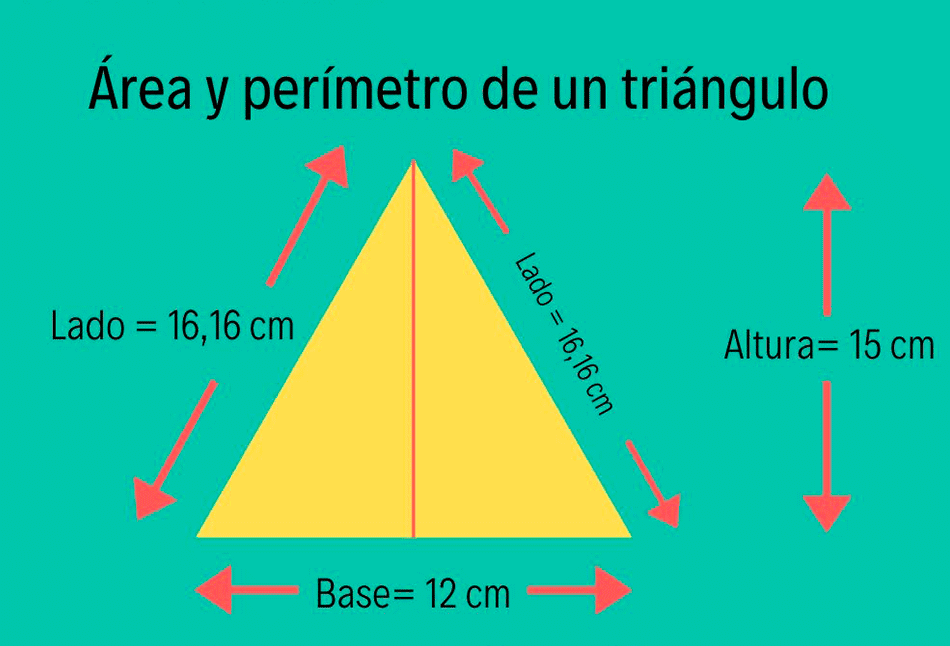
Cómo sacar el área de un triángulo
Calcular el área de un triángulo es un cálculo básico que se suele hacer en álgebra o geometría. Gracias a esta guía puedes aprender con facilidad y rapidez cómo sacar el área de un triángulo.
Paso a paso
- Paso 1: Obtener los lados del triángulo.
- Paso 2: Calcular la semiperímetro (S), que se obtiene por la siguiente formula: S = (a + b + c)/2, dónde ‘a’, ‘b’ y ‘c’ son los lados del triángulo.
- Paso 3: Calcular el área del triángulo (A) con la siguiente formula: A = √(s(s-a)(s-b)(s-c)).
Ejemplo práctico con cálculos
Supongamos que tenemos un triángulo con los lados ‘a’ = 8, ‘b’ = 5 y ‘c’ = 7. Para obtener el área del triángulo seguimos los tres pasos arriba descritos:
- Paso 1: Los lados del triángulo son ‘a = 8’, ‘b = 5’ y ‘c = 7’.
- Paso 2: Calcular la semiperímetro (S). S = (a + b + c)/2. Entonces, S = (8 + 5 + 7)/2 = 10
- Paso 3: Calcular el área del triángulo. A = √(s(s-a)(s-b)(s-c)). Entonces, A = √(10(10-8)(10-5)(10-7)) = 17,3.
Por lo tanto, el área del triángulo es 17,3.
¿Cómo calcular el área de un triángulo rectángulo?
Area de un Triangulo Rectangulo – YouTube
Para calcular el área de un triángulo rectángulo, primero deberás determinar la base y la altura. La base debe ser un lado del triángulo rectángulo. La altura debe ser perpendicular a la base. Después, multiplica la base por la altura. La fórmula es area = (base x altura) / 2. Por ejemplo, para un triángulo de base 9 y altura 4, el área sería (9 x 4) / 2 = 18.
¿Cómo se puede sacar el área de un triángulo?
El área de un triángulo es igual a base por altura partido por 2. La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación). La base es la longitud de cualquier uno de los lados del triángulo. La formula es:
Área = (Base Altura) / 2
¿Cómo calcular el área de un triángulo con sus lados?
Área del triángulo conociendo los tres lados | FÓRMULA DE HERÓN
El área de un triángulo dada la longitud de sus tres lados se puede calcular con la Fórmula de Herón. Esta fórmula fue creada por Herón de Alejandría (aún antes de Cristo). La fórmula es la siguiente:
A=√(s(s-a)(s-b)(s-c))
Donde:
A= área del triángulo
s= semiperímetro del triángulo
a, b, c= longitud de los tres lados del triángulo
Ejemplo:
Supongamos que tenemos un triángulo con lados de 12 cm, 6 cm y 8 cm respectivamente.
Entonces el semiperímetro del triángulo s= (12+6+8)/2 = 13
Y el área del triángulo A=√(13(13-12)(13-6)(13-8))
A=√(13(1)(7)(5))
A=√455
A = 21,22 cm²