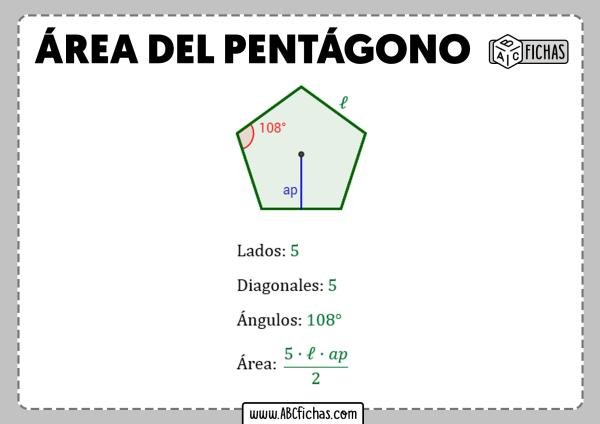
Cómo sacar el área de un pentágono regular
Un pentágono regular es una figura geométrica con cinco lados iguales y ángulos iguales. Se puede aplicar el siguiente método para calcular el área total de un pentágono regular:
Método de cálculo
- Paso 1: Calcular el lado del pentágono.
- Paso 2: Calcular el perímetro del pentágono.
- Paso 3: Dividir el perímetro entre 5 para obtener el apotema.
- Paso 4: Multiplicar el lado por el apotema para obtener el área total.
Ejemplo de cálculo
Si un pentágono tiene un lado de 10 cm, su perímetro será de 50 cm. Si dividimos el perímetro entre 5 obtenemos un apotema de 10 cm. Por lo tanto, el área total del pentágono es igual a 10 cm multiplicado por 10 cm, es decir 100 cm2.
¿Cómo calcular el área de un pentagono regular sin el apotema?
Área de un Pentágono SIN apotema – YouTube
Para calcular el área de un pentágono regular sin el apotema, primero necesita conocer la longitud de uno de los lados (a). A continuación, aplique la siguiente fórmula:
área = (1/2) × (5 × a2) × Cotangente (54 grados).
Aquí, Cotangente (54 grados) tendrá un valor constante de 1.72047. Por lo tanto, la fórmula final para calcular el área de un pentágono regular sin el apotema sería:
área = (1/2) × (5 × a2) × 1.72047
¿Cómo calcular el área y el perímetro de un pentágono regular?
Como todos los lados están medidos en centímetros, sólo sumamos las longitudes de los 3 lados para obtener el perímetro….
Para calcular el área de un pentágono regular primero necesitas encontrar el radio (R). El radio es la distancia desde el centro del pentágono al centro de uno de los lados. Para encontrar el radio, multiplica la longitud de los 5 lados por dos y divide el resultado por la cincoava parte de la circunferencia (2π). El resultado será el radio del pentágono.
A continuación, multiplica el radio por 5 para obtener la longitud de los lados del pentágono. Sumamos los 5 lados para obtener el perímetro del pentágono.
Finalmente, para calcular el área del pentágono, necesitarás la apotema. Esta es la distancia desde el centro del pentágono al centro de uno de los lados. Para encontrar la apotema, elevamos el radio al cuadrado y divide el resultado por el doble del producto de un lado por el seno del ángulo central. Multiplica la apotema por el perímetro para obtener el área del pentágono.
¿Cuál es la fórmula del pentágono?
Perímetro y área de un pentágono Perímetro (P): Sumamos los lados del polígono, es decir: P=AB+BC+CD+DE+AE. Si el pentágono es regular y todos los lados tienen longitud L, se cumple que P=5L.
Área (A): Utilizamos la fórmula de Herón. Si sabemos los lados del pentágono, obtenemos sus semiperímetro con S=(AB+BC+CD+DE+AE)/2. A continuación, calculamos los cinco ángulos internos al igual que sus áreas con A1=(S-AB)(S-BC)(S-CD)(S-DE)(S-AE). Finalmente, para calcular el área del pentágono necesitamos multiplicar A1 por el seno del ángulo central al pentágono. Por tanto, el resultado se cumple con A=A1sen(α).
Cómo Sacar El Área Del Pentágono Regular
El área de un pentágono es un cálculo matemático importante para muchas áreas como la construcción. El pentágono es una figura geométrica con cinco lados y cinco ángulos. Aprender a calcular el área de un pentágono es fácil y cualquiera con un poco de conocimiento de geometría puede hacerlo.
Pasos para calcular el área del pentágono regular:
- Paso 1: Calcule el perímetro del pentágono. Esto se calcula sumando la longitud de cada lado.
- Paso 2: Calcule la apotema, que es la distancia medida desde el centro hasta cualquier lado.
- Paso 3: Multiplique el perímetro por la apotema y divida el resultado entre 2.
- Paso 4: El resultado es el área del pentágono.
Ejemplo:
Supongamos que el pentágono regular tiene un perímetro de 40 metros y una apotema de 5 metros.
- Paso 1: El perímetro es 40 metros
- Paso 2: La apotema es 5 metros.
- Paso 3: 40 × 5 = 200; 200 ÷ 2 = 100 metros cuadrados.
- Paso 4: El área del pentágono es de 100 metros cuadrados.
Esta misma fórmula se usa para calcular el área de todos los pentágonos regulares. Asegúrate de tener los datos correctos antes de calcular el área para obtener un resultado preciso.