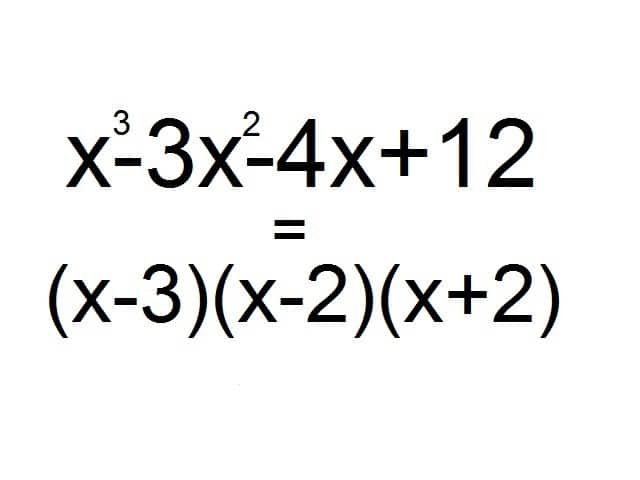Factorizar una ecuación de tercer grado
Factorizar una ecuación de tercer grado es un tema importante de matemáticas sobre el cual solucionar los problemas. Consiste en encontrar todos los factores de los términos (+y -) que están presentes en la ecuación. Estos factores se usan para simplificar y desarrollar la ecuación. Si se hace correctamente, se pueden obtener los resultados de la ecuación de manera mucho más fácil.
Cómo factorizar una ecuación de tercer grado
En primer lugar, es importante tener en cuenta el grado de la ecuación. Los factores siempre serán números enteros, tal vez un número racional. Por lo tanto, para comenzar a factorizar una ecuación de tercer grado, los factores se encontrarán dentro de los siguientes grupos:
- Primos
- Grupos
- Productos
También es importante considerar el coeficiente de los términos. Para encontrar los factores de los términos, debe determinar el menor común múltiplo de los términos y usar los factores primos para encontrar los productos. Después de haber encontrado los factores, reúnalos para formar los grupos y elimine los términos innecesarios.
Una vez que se hayan encontrado y organizado los factores de los términos en los grupos, puede pasar a desarrollar la ecuación. Utiliza el Binomio de Newton para desarrollar la ecuación y simplemente desarrolla el binomio para cada factor. Finalmente, suma los términos para obtener los resultados finales.
La factorización de una ecuación de tercer grado puede parecer complicada, pero es solo una cuestión de saber cómo encontrar los factores correctos y organizarlos correctamente. Si sigues estos pasos, puedes desarrollar una ecuación con facilidad.
¿Cómo reducir un polinomio de grado 3?
Factorización, polinomio de grado 3 con el método de agrupación de …
La factorización puede realizarse de la siguiente manera:
1. Agrupe los términos: Agrupe los términos con el mismo factor común, en este caso, los términos con el factor x. Esto creará tres grupos, uno para cada exponente.
2. Simplifique cada grupo: Simplifique cada grupo de términos para crear una sola expresión polinomial con los mismos factores.
3. Utilice los productos de notación factorial para reducir los términos: Utilice el producto de notación factorial para reducir los términos en la expresión, lo que le permite convertir la expresión en su forma factorizada.
Por ejemplo, el polinomio x3+ 3×2 – 8x – 24 está formado por los factores x, x2 y x3. Así que si los agrupamos, obtenemos:
x3 + 3×2 – 8x – 24
= x3 + x(3×2 – 8) – 24
= x3 + x(x2 – 8) – 24
= x(x2 + x – 24)
= x(x – 8)(x + 3)
Entonces, el polinomio de grado 3 se ha reducido por factorización.
¿Cómo se factoriza una ecuación de tercer grado?
ECUACIONES DE TERCER GRADO – Ejercicio 3 – YouTube
Para factorizar una ecuación de tercer grado, hay que tener en cuenta la forma de la ecuación de tercer grado:
ax^3 + bx^2 + cx + d = 0
En primer lugar, se debe localizar el factor común más grande. Esto se puede lograr dividiendo por el coeficiente a (el término a la izquierda) los otros tres términos.
x^3 + (b/a)x^2 + (c/a)x + (d/a) = 0
A partir de ahí, se debe factorizar como una suma de un trinomio y un binomio. Esto se hace multiplicando los términos del binomio iguales aunque sean polinomios.
x^3 + (b/a)x^2 + (c/a)x + (d/a) = (x^2 + (c/b)x + d/b ) + (x + (a/b))
Después de esto, se debe emplear el método de factorizar para la parte binomio, lo cual se puede hacer factorizando x al igual que los términos y después trabajando con la parte trinomio usando las fórmulas de factorización por paréntesis
x^3 + (b/a)x^2 + (c/a)x + (d/a) = (x(x + (c/b)) + (d/b)) + (x + (a/b))
Finalmente, se debe volver a colocar los términos desde los cuales se inició la factorización
x^3 + bx^2 + cx + d = (x(x + c/b) + d/b) + (x + a/b)
¿Cómo resolver ecuaciones de grado 3?
La forma tradicional de resolver una ecuación cúbica es reducirla a una ecuación cuadrática y luego resolverla mediante la factorización o la fórmula cuadrática. Al igual que una ecuación cuadrática tiene dos raíces reales, una ecuación cúbica puede tener posiblemente tres raíces reales.
Cómo factorizar una ecuación de tercer grado
Qué es una ecuación de tercer grado
Una ecuación de tercer grado es una ecuación de grado superior a 2, y con un término independiente no nulo. Esto significa que tendrá una forma general como x3 + bx2 + cx + d = 0. Estas ecuaciones se pueden resolver con diferentes tipos de métodos matemáticos como factorización, sustitución o descomposición en fracciones parciales.
Deconstrucción de la ecuación
Paso 1: Primero, es necesario trabajar con todos los términos de la ecuación hasta reacomodarlos para poder factorizar correctamente. Esto significa desacoplar los términos de la parte izquierda de la ecuación en tres términos separados como se muestra a continuación:
- x3 = x3
- bx2 = b(x2 – x2)
- cx + d = (cx – cx) + d
Paso 2: Ahora, tenemos que factorizar la ecuación. Para ello, es necesario multiplicar todos los términos de la izquierda de la ecuación por un factor común, es decir, x2. Esto nos dará la siguiente ecuación:
- x3 + bx2 – bx2 + cx2 – cx2 + dx2 = 0
Paso 3: Ahora, es necesario agrupar los términos de la izquierda de la ecuación. Esto significa qeu se agruparán los términos de la forma (ax2 + bx + c)(dx + e). La ecuación se verá así después del proceso de agrupación:
- x3 + (b + c – d)x2 + (c – d + e)x – e = 0
Paso 4: Finalmente, es necesario encontrar los valores de los coeficientes a, b, c, d y e para poder factorizar completamente la ecuación y así encontrar sus raíces. Esto significa que debemos hallar los valores de los coeficientes tales que (b+c-d)=0, (c-d+e)=0 y e=0, para lo cual utilizaremos sustitución.
Encontrando los valores de los coeficientes a, b, c, d y e,entonces la ecuación queda factorizada de la siguiente forma:
- (x – a)(x2 + bx + c) = 0
Una vez factorizada esta ecuación, podemos resolverla usando diferentes métodos como la sustitución o la división sintética.